Bugünkü makalemizde basit faiz hakkında bilgiler vereceğiz. Belirli bir süre boyunca belirli bir miktar para ödünç aldığımız zaman, borcumuzu faiz olarak bilinen bir ücretle birlikte geri ödeyeceğimizi kabul ederiz. Benzer şekilde, bir tasarruf hesabına bir miktar para yatırdığımızda, hesap bize faiz kazandırır. Bu ders, basit faiz adı verilen belirli bir faiz türünün nasıl hesaplanacağını gösterecektir.
Basit Faiz Nedir?
Basit faiz, geçmiş faiz (ücretli veya borçlu) veya diğer finansal hususlar gibi başka faktörler dikkate alınmaksızın, kredinin tamamı boyunca ödünç alınan veya yatırılan tutara uygulanan bir faiz türüdür. Finansal şirketler tarafından yönetilen kısa vadeli kredilere, genellikle bir yıl veya daha kısa sürede basit faiz uygulanır. Aynı şey, benzer şekilde kısa bir süre için yatırılan para için de geçerlidir.
Basit faiz oranı bir orandır ve tipik olarak yüzde olarak ifade edilir. Bir krediye veya yatırıma olan faiz miktarını belirlemede önemli bir rol oynar. Alınan veya kazanılan faiz tutarı, bir sonraki inceleyeceğimiz üç önemli miktara bağlıdır.
Basit Faiz Formülü
Serap’ın mobilya satın alabilmesi için 2.000 TL ödünç alması gerekiyor. İki farklı kredi için onaylandı. Kredi 1, ödünç aldığı günden tam bir yıl sonra 2.200 TL iade ederek krediyi ödemesi şartıyla şimdi 2.000 TL borç almasına izin veriyor. Kredi 2, yıllık% 7 faiz oranıyla bir yıllık benzer kredi dönemi ile 2000 TL ‘lik ön ödeme de sunuyor. Serap için hangisi daha iyi?
Ödünç alınan veya yatırılan tutara anapara denir. Yukarıdaki örneği kullanarak, Serap mobilya satın almak için 2,000 TL ödünç aldığında, anaparanın 2,000 TL olduğunu söylüyoruz.
Finansal kurumların faiz oranı olarak adlandırılan bir tutarı yüzde olarak belirtmesi gelenekseldir . Bu faiz oranı, ödünç alınan veya yatırılan anapara oranını temsil eder. Tipik olarak, bu faiz oranı yıllık yüzde olarak verilir, bu durumda yıllık faiz oranı olarak adlandırılır . Örneğin, yıllık% 5 oranında 100 TL borç alırsak, yıl sonunda 100 $TL ‘lik % 5 veya 5 TL’ lik borçlandırılacağımız anlamına gelir.
Kredi süresi veya süresi anapara tutarı ya ödünç ya da yatırım olduğu zamandır. Genellikle yıllar içinde verilir, ancak bazı durumlarda aylar hatta günler içinde alıntılanabilir. Bu durumda, ay veya gün olarak verilen bir dönemden yıllara bir dönüşüm gerçekleştirmemiz gerekir.
Basit faiz formülü bize hesaplamak için izin verir I kazandığı veya kredi tahsil ilgi. Bu formüle göre, faiz tutarı P = asıl olduğu I = Prt ile verilir , r ondalık formda yıllık faiz oranıdır ve t yıl cinsinden ifade edilen kredi dönemidir.
Basit Faiz Örnekleri
Serap’ın aldığı ikinci teklif, t = 1 yıl boyunca yıllık% 7 oranında P = 2.000 TL ana para ödünç almaktır . R oranı bir yüzde değerinden ondalık biçime dönüştürülmelidir, yani r = 0.07 elde etmek için yüzde değerini% 7’ye 100’e böleriz.
Şimdi, henüz tarif edilen kredi teklifini kabul ederse Serap’ın borçlandırılacağı faiz miktarını hesaplıyoruz:
I = Prt = (2.000) (0.07) (1) = 140 TL.
Örneğimizden sonra, Serap ikinci krediyi kabul ederse, bankaya borçlu olacağı faizin 140 TL olduğunu belirledik. Peki, Serap borcunu ödemek için bankaya ne kadar ödemek zorunda kalacaktı? Ödünç aldığı parayı veya 2.000 TL olan anaparayı geri ödemek zorunda kalacaktı ve bankaya hesapladığımız faizi ödemek zorunda kalacaktı, ki bu da ben = 140 TL. Böylece, bankaya 2.000 TL + 140 TL borçlu olacak ve bu da 2.140 TL ‘e eşit olacak. Serap’ın Kredi 1’i kabul etmesi durumunda hala ödemek zorunda olduğu 2.200 TL’den daha az olduğunu not ediyoruz. Açıkçası, Kredi 2 daha iyi bir seçimdir.
Vade Değerinin Geleceği
Kredi alırken geri ödememiz gereken toplam tutara , kredinin gelecekteki değeri denir. Gelecekteki değer için başka bir isim vade değeridir. Gelecekteki değeri, A , bir kredinin denklemi tarafından verilen A = P + I . Anapara tutarı ( P ) yatırdığımızda , gelecekteki değer ( A ) basit faiz uygulandıktan sonra kredi döneminin sonunda sahip olacağımız toplam tutarı temsil edecektir.
Faiz formülünü I = Prt kullanarak, A = P + Prt veya sağ taraftaki P’yi çarpanlarına ayırdıktan sonra , A = P (1 + rt) gelecekteki değer için bir formül türetebiliriz .
Örnek 1
Aslı, altı ay içinde geri ödenmesi için yıllık% 3.25 faiz oranıyla yerel bankasından 300 TL borç alıyor. Kredinin sonunda ne kadar faiz ödeyecek?
Çözüm
Aşağıdaki değerler verilmiştir: anapara tutarı, P = 300, yıllık faiz oranı, r =% 3.25 ve yıl cinsinden t kredi dönemi . Kredi süresi altı aydır, bu nedenle altı ay 12 yıl, bir yıldaki ay sayısı ile hesaplanarak t = ½ elde edilir.
t = ay cinsinden kredi dönemi / yılda 12 ay = 6/12 = 1/2
R değeri, bir yüzde olarak ondalık biçime dönüştürülerek belirlenir:
r = yüzde olarak yıllık oran / 100 = 3.25 / 100 = 0.0325
Şimdi kredinin sonunda ödenecek faizi belirlemek için I = Prt faiz formülünü kullanıyoruz :
I = Prt = (300) (0.0325) (1/2) = 4.875
Bu değer, banka tarafından daha karlı olduğu için 4.88 TL ‘e yuvarlanacaktır. Bu nedenle Aslı’nın faiz için 4.88 TL geri ödemesi gerekecek.
ÖRNEK 2
105 gün içinde geri ödenecek yıllık% 10.5 faiz oranıyla 4.000 TL’lik basit faiz kredisi için vade değerini bulun. Bankaların yılda 360 gün olduğunu varsaymaları yaygın bir uygulamadır.
Çözüm
Bize asıl tutar verilir, P = 4.000. Yıl cinsinden kredi süresi 105 günü 360 güne bölerek hesaplanır, bu da bize t = 21/72 verir .
t = 105/360 = 21/72
Yıllık faiz oranı% 10.5 veya ondalık formda r = 0.105’tir.
Kredinin vade değeri A = P (1 + rt) formülüyle verilmiştir . Dolayısıyla, elimizde:
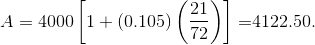
Bu nedenle, bu kredinin gelecekteki değeri 4.122.50 TL ‘dir.
ÖRNEK 3
Ali bir tasarruf hesabına 3.000 TL yatırım yapıyor. Bir yıl sonra, hesap 33,00 TL faiz kazandı. Yıllık basit faiz oranı nedir?
Çözüm
Bize anapara tutarı, P = 3.000 TL, faiz, I = 33.00 ve yıl cinsinden kredi süresi t = 1 olarak verilmiştir. Faiz oranı, r için çözülen basit faiz formülü I = Prt’den belirlenir :
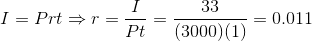
Bu nedenle, yıllık basit faiz oranı% 1,1’dir.
Ders Özeti
Anapara adı verilen toplam para ödünç verilen kısa vadeli kredilere genellikle basit faiz uygulanır. Kredi döneminin sonunda anapara tutarına faiz uygulanır ve kredi, katlanılan anaparaya ek olarak, ödünç alınan anapara tutarı ödenerek ödenir. Faiz tutarı, anapara tutarı, yıllık yüzde olarak verilen yıllık faiz oranı ve anapara tutarının ödünç alındığı veya yatırıldığı zaman olan kredi süresi ile orantılıdır.
Basit faiz formülü I = Prt’dir .
Gelecekteki değer A = P (1 + rt) formülüyle belirlenir .
Anahtar terimler
- Basit Faiz : Kısa vadeli krediye uygulanan kredi tutarına, kredi süresince uygulanan faiz tutarı
- Anapara Tutarı : ödünç alınan veya yatırılan tutar
- Yıllık Faiz Oranı : Yıllık yüzde olarak verilen faiz oranı
- Kredi Dönemi : kredinin geri ödenmesi gereken süre
- Gelecekteki Değer : kredi döneminin sonunda anapara tutarı ve faiz dahil geri ödenecek tutar.





